この定理は今から2500年ぐらい前に活躍した「ピタゴラス」っていう数学者が発見した定理だから、 最新 三 平方 の 定理 難問 中学3年生 数学 三平方の定理平面図形への活用 練習問題 Studydoctor三平方の定理の応用問題中学3年数学 Studydoctor 中学3年生 数学 *1 三平方の定理(ピタゴラスの定理)については、拙書『大人のための中学数学勉強法 』に詳しく書きました。一部を抜粋します。 三平方の定理(ピタゴラスの定理)の誕生秘話 ピタゴラスはギリシャのサモス島というところで生まれました。このサモス島のヘーラー神殿というところが成り立ちます。これで、三平方の定理を証明することができました!「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。

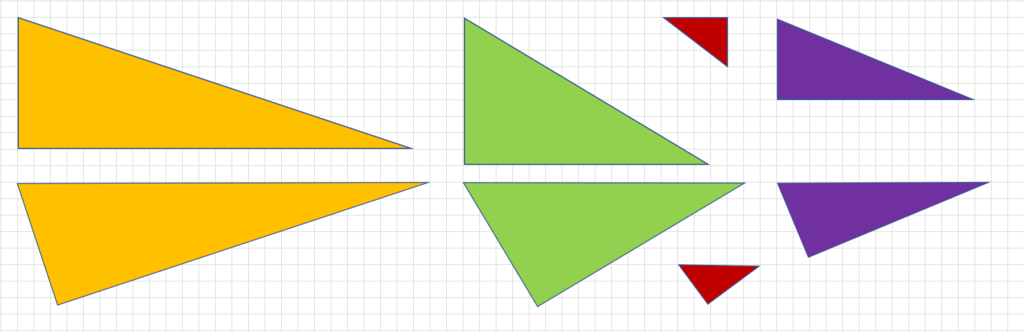
三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト
三 平方 の 定理 は ピタゴラス
三 平方 の 定理 は ピタゴラス-三 平方 定理 計算 三平方の定理(ピタゴラスの定理) 三平方の定理をご存知でしょうか?ピタゴラスの定理と言った方がピンとくるかもしれません。これは、直角三角形の二辺の長さが分かっていれば、残りの一辺の長さを求めることが出来るものです 三角形の三辺をa,b,cとし、斜辺がcとするとc^2=a^2b^2となる。三平方の定理はピタゴラスの定理とも呼ばれる 三平方の定理がわからない人へ 中3数学「三平方の定理」がわからない人は、以下の順でTry ITの映像授業を観て勉強してみてください。




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
中3数学平方根、ルートの値を語呂合わせ!覚え方まとめ 3分でわかる!三平方の定理(ピタゴラスの定理)の公式とは 三平方の定理 無料で使える中学学習プリント;この定理の逆も成り立つ。すなわち、三角形の1辺の平方が他の2辺の平方の和に等しければ、始めの辺に対する頂角は直角である。この逆定理の成立によって、たとえば、辺の長さが3、4、5である三角形は3 2 +4 2 =5 2 であるから、直角三角形となる。この3ピタゴラスの定理とも言われます。 三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。 この三平方の定理を活用すると、直角三角形の2辺がわかれば残りの1辺の長さを計算することができます。
b2=c2 が成り立ちます.これを「 三平方の定理 」といいます. 見かけ上「 斜めに見えている辺 」が斜辺なのではない 「 直角の向かい側 」にある辺=「 一番長い辺 」が斜辺 例1 直角をはさむ2辺の長さが与えられると斜辺の長さが求まります. 3222「ユークリッド原論」の「三平方の定理」は始めから「ピタゴラスの定理」 と呼ばれたわけではありません。このように呼ばれるようになったのは 「ユークリッド原論」が書かれてから数世紀が経過してからです。 プロクロス (Proclus, 412~485) は3分でわかる!三平方の定理(ピタゴラスの定理)の公式とは 三平方の定理(ピタゴラスの定理)の証明まとめ5選全部で 三平方の定理 特別な直角三角形の3辺の比|中学生からの 数学三平方の定理が成り立つ三辺の比:最重要7パターン
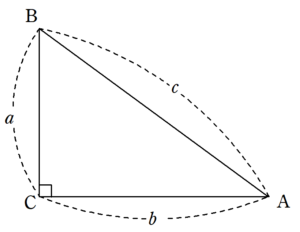
定理 直角三角形の直角をはさむ2辺の 長さをα, ら,纂通の長さをcと すれば,次の関係が成り立つ。 α2ら2=c2 図21 現在の中学校教科書のビタゴラスの定理 現在のピタゴラスの定理は, このように直角三角形の三辺の関係として表現三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



これなら小学生でも分かる 水で車輪を使って ピタゴラスの定理 を証明する実験動画 コモンポストムービー




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
三平方の定理(ピタゴラスの定理): \angle C=90^ {\circ} ∠C = 90∘ であるような直角三角形において, a^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べて正方形ABDFをつくる。 正方形ABDFの面積をSとすると、1辺がcなので S=c2 ① また、正方形ABDFは△ABCと合同な三角形4つと正方形EGHCでできている。という関係が成り立つ。 この関係を 三平方の定理 または ピタゴラスの定理 と言う。



投稿1036



三平方の定理の証明 ピタゴラスの証明 Fukusukeの数学めも
ピタゴラスの定理ピタゴラスのていりPythagorean theorem 三 平方 の 定理 ともいう。 直角三角形 において, 直角 である 頂角 の対辺の 長さ の平方は,他の2辺の平方の和に等しいという定理。 いま三角形 ABC において,∠C=∠R (直角) ,各頂角の対辺の長さ三平方の定理は ピタゴラスの定理 とも呼ばれ、三平方の定理の式( $a^2b^2=c^2$ )は、直角三角形の辺の長さを求めるときによく使われています。初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 1 2 3。



三平方の定理




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。 このピタゴラスの定理(三平方の定理)の証明は、百以上知られている。これに対して、三平方の定理の逆とは?? そもそも、なぜ三平方の定理(ピタゴラスの定理) 三平方の定理をご存知でしょうか? ピタゴラスの定理と言った方がピンとくるかもしれません。 これは、直角三角形の二辺の長さが分かっていれば、残りの一辺の長さを求めることが出来るものです。 斜辺(一番長い辺)の長さを求める場合は、残り二辺の自乗したものをたす。 他の二辺を求める場合は、斜辺の自乗したものピタゴラスの定理(3平方の定理)とは ピタゴラスの定理っていうのは、 直角三角形の3辺の長さの関係を表したものだよ その関係っていうのは、$斜辺^2=底辺^2高さ^2$だよ 辺の長さを求める時は、この式に当てはめることで求めることが 三平方の定理の証明!




三平方の定理 ピタゴラスの定理 東大合格コム



ベクトルの長さを三平方の定理を使って求める
壁紙 押入れ トップ 100 三 平方 の 定理 表 3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく 数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 となります。 となります。 が成り立ちます。 これを「三平方の定理」 といいます。★三平方の定理を満たす3 つの自然数の組をピタゴラス数と言います。 三平方の定理だけでなく、ピタゴラス数もインド以外のその他各地で発見・ 利用されています。 三平方の定理の発見されていたギリシア・中国はもちろん、そのほかにも・・・



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
ピタゴラスの定理(三平方の定理)を使うと, a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 を満たす自然数の組 ( a , b , c ) (a,b,c) ( a , b , c ) をピタゴラス数と呼ぶ。




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理を英語で読んでみる




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張



1
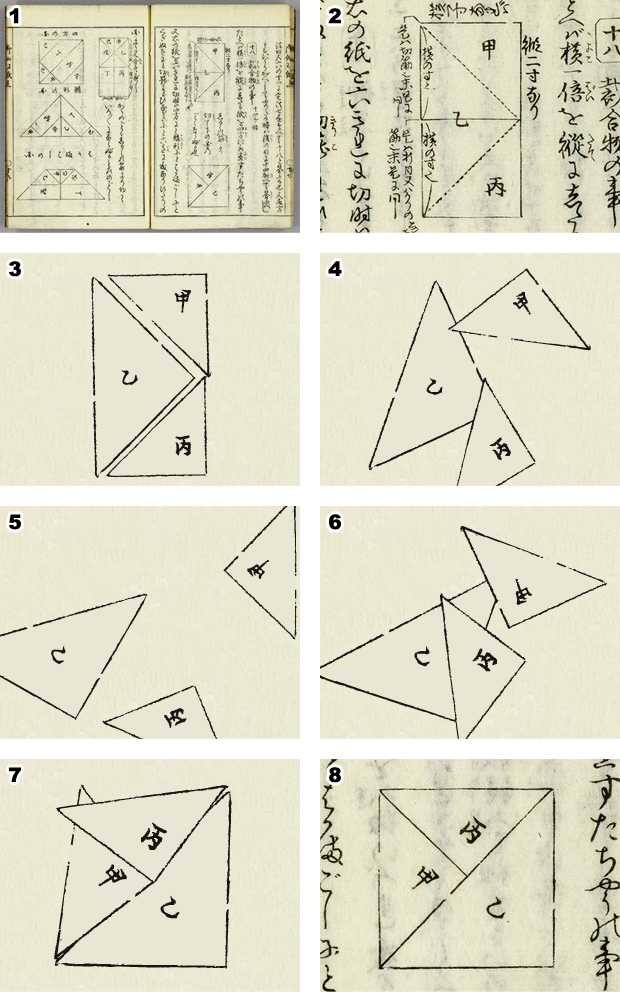



コラム ピタゴラスの定理 江戸の数学




ピタゴラスの定理 三平方の定理の写真 画像素材 Snapmart スナップマート




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook




ピタゴラスの定理 Wikipedia




数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube




三平方の定理 がひと目で分かる展示が面白いと話題に 視覚的にわかる こういうのが学校にあったら ねとらぼ
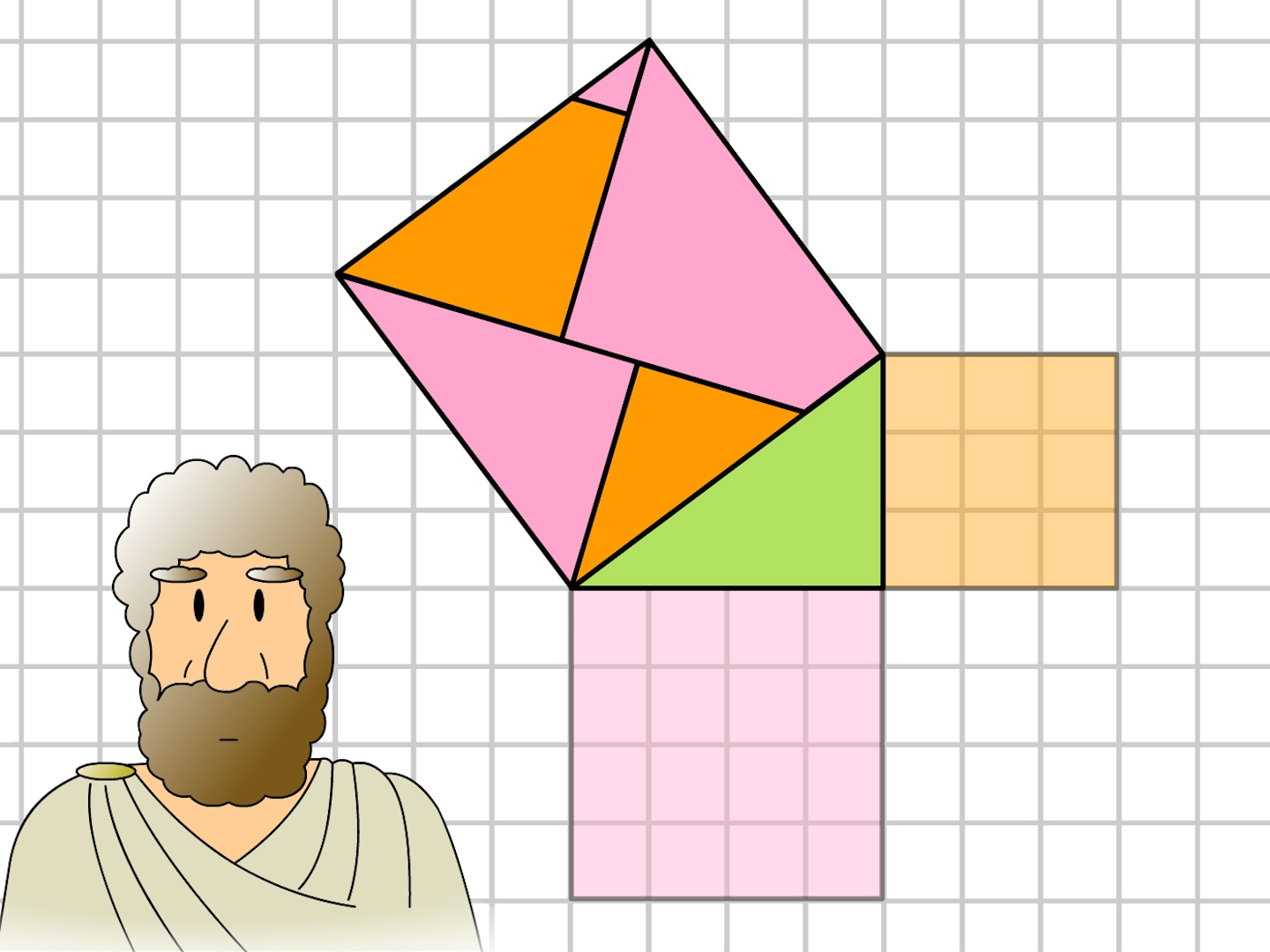



3年 ピタゴラスの定理 数学イメージ動画集 大日本図書




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
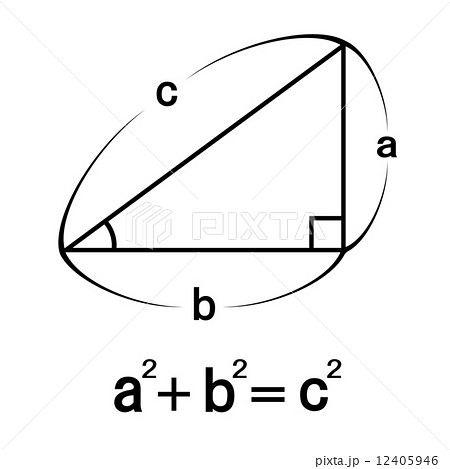



三平方の定理のイラスト素材




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理で辺を求める Youtube
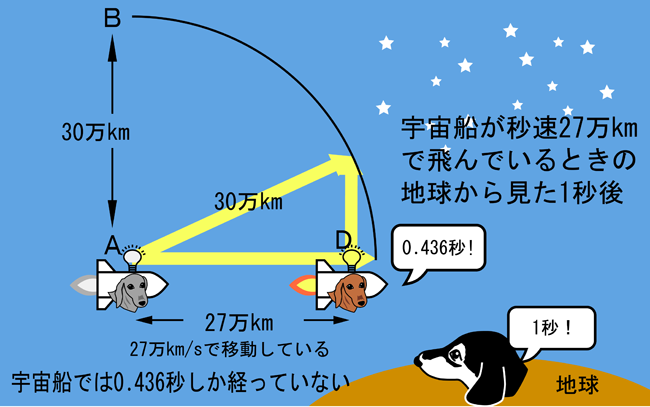



三平方の定理でわかる特殊相対性理論 光速度不変 ふっさんブログ




三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生




三平方の定理 ピタゴラスの定理
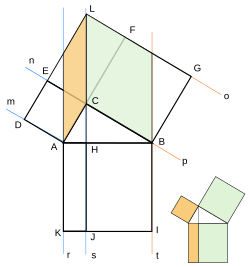



ピタゴラスの定理 Wikipedia
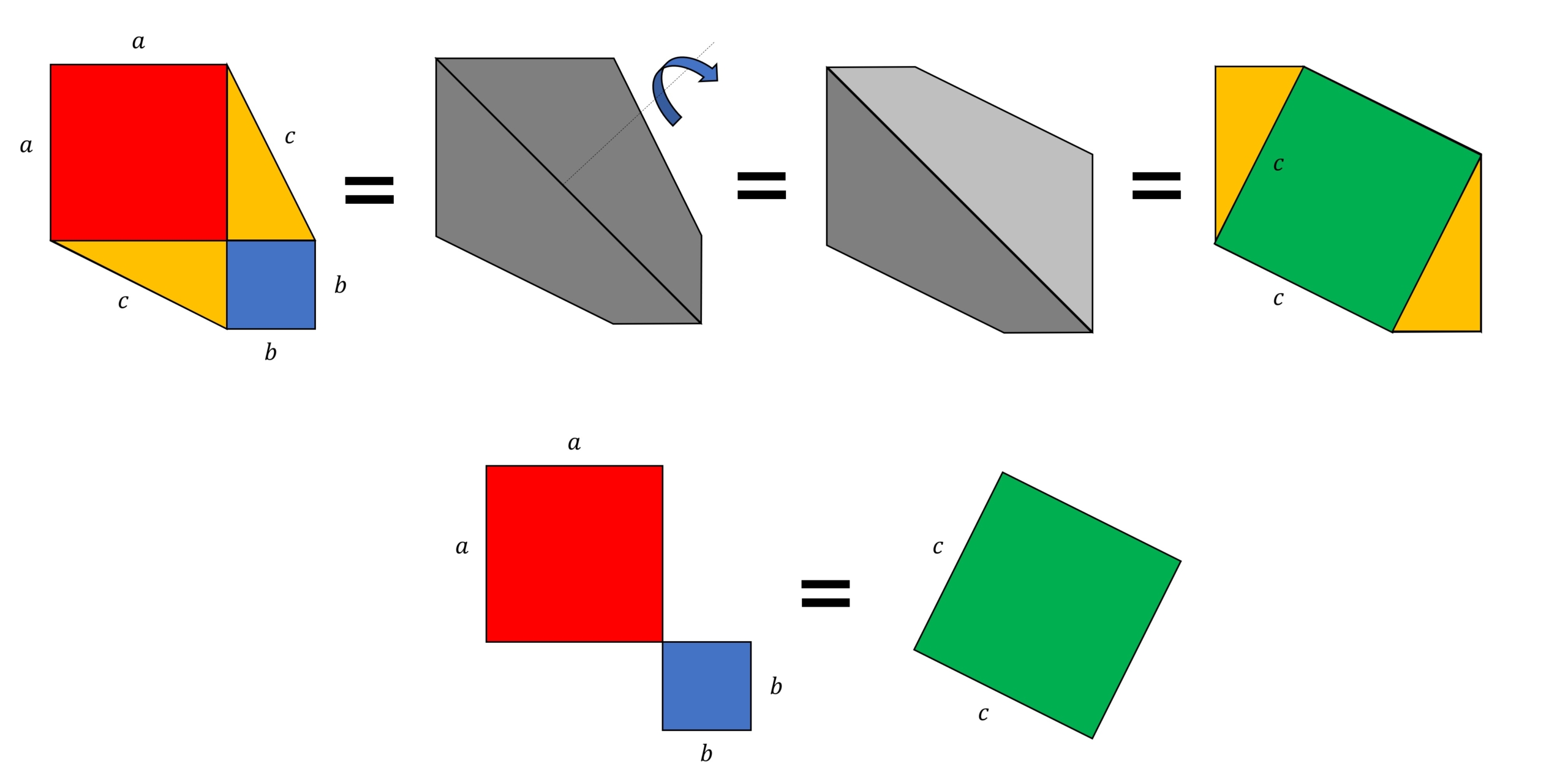



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



三平方の定理




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張
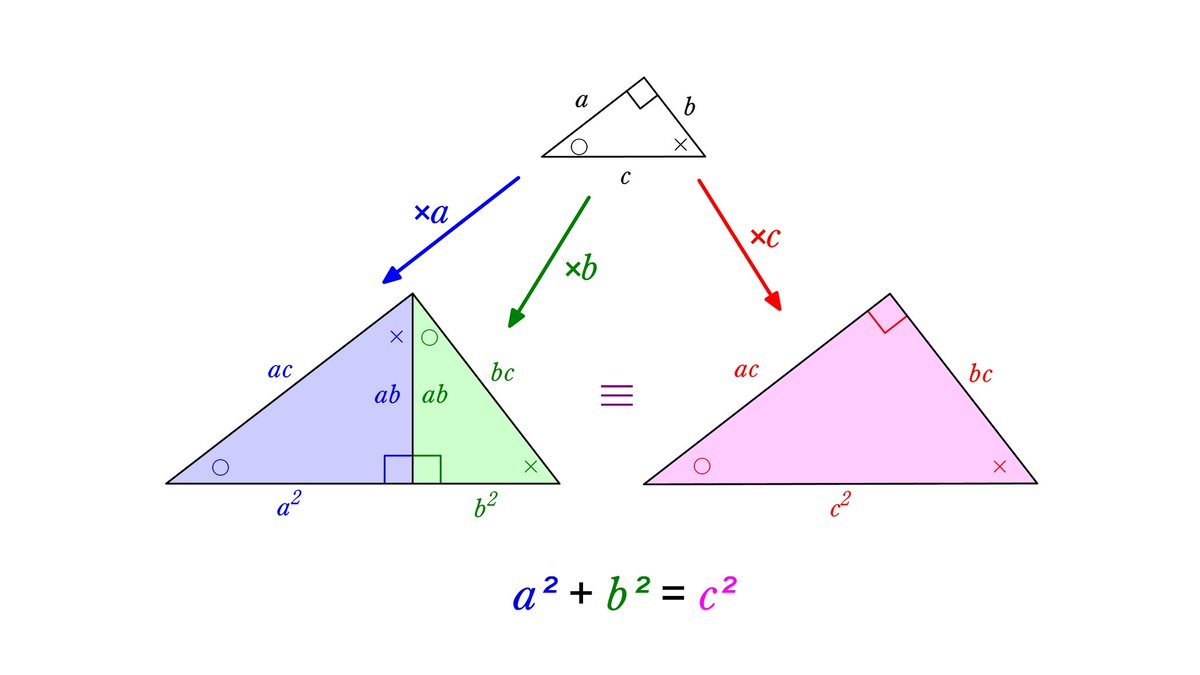



三平方の定理
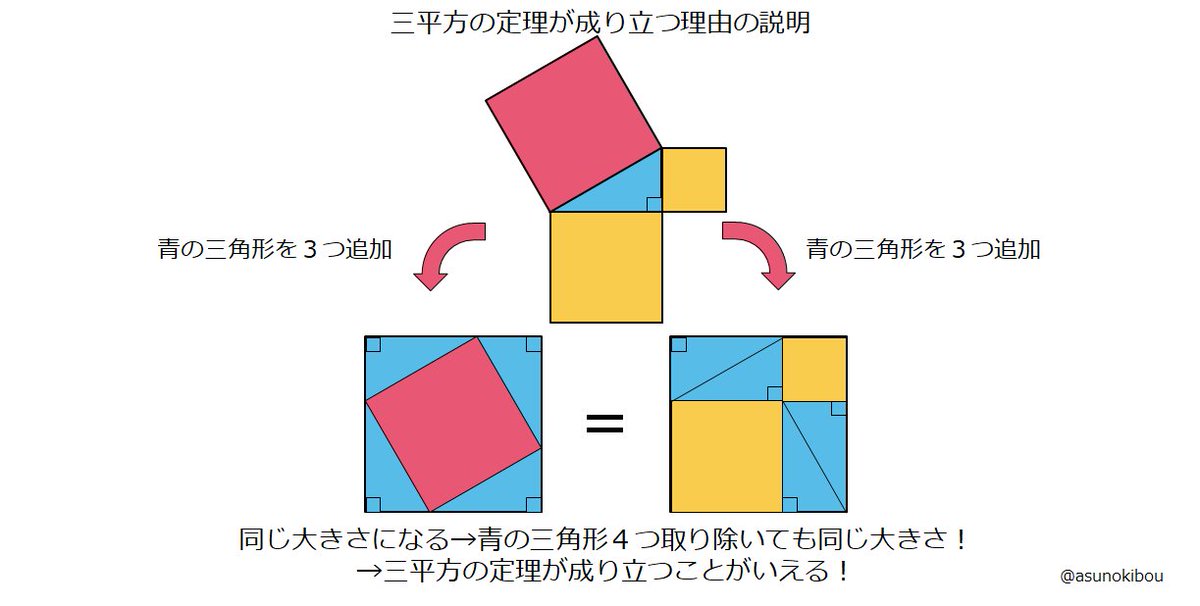



三平方の定理 ピタゴラスの定理 を分かりやすく表した動画 Togetter



三平方の定理




コラム ピタゴラスの定理 江戸の数学




Spoxc6l2pfbrwm




三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
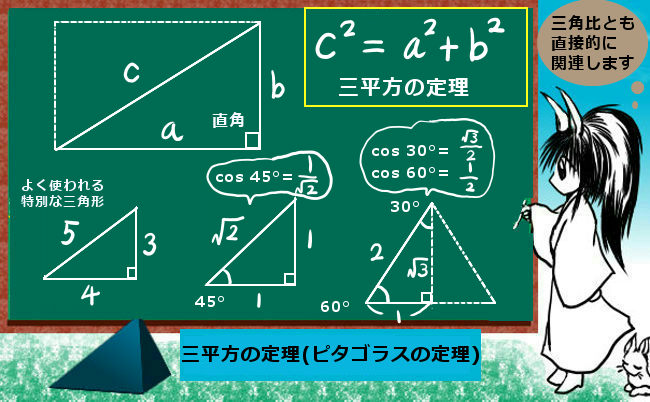



三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理 ピタゴラスの定理 と証明 Rikeinvest




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
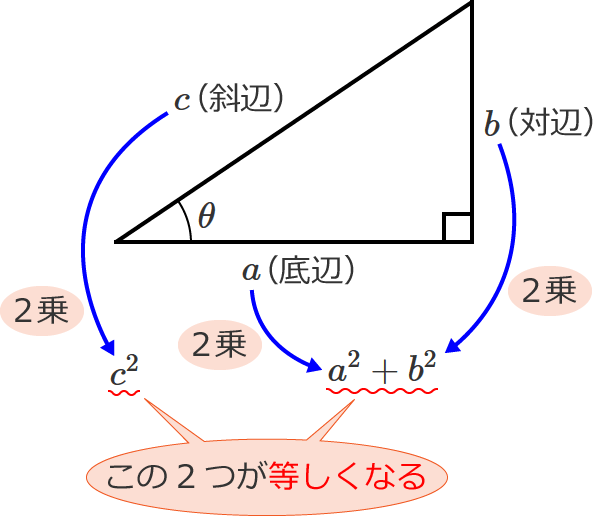



三平方の定理 ピタゴラスの定理




三平方の定理の証明 方べきの定理の利用1 Fukusukeの数学めも




三平方の定理 自動計算サイト
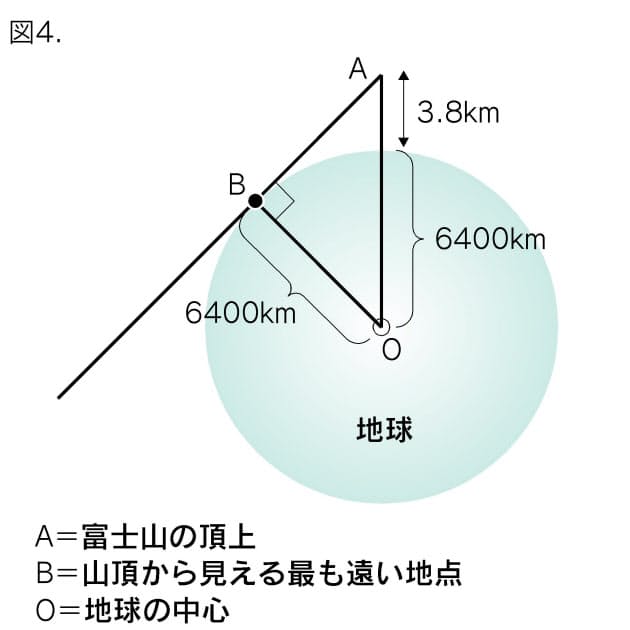



富士山やスカイツリーからどこまで見渡せるか 川の対岸までの距離 渡らずに知る方法 Nikkei Style
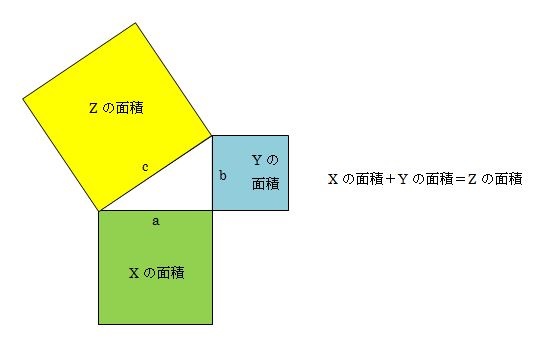



三平方の定理 もう一度やり直しの算数 数学




中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット
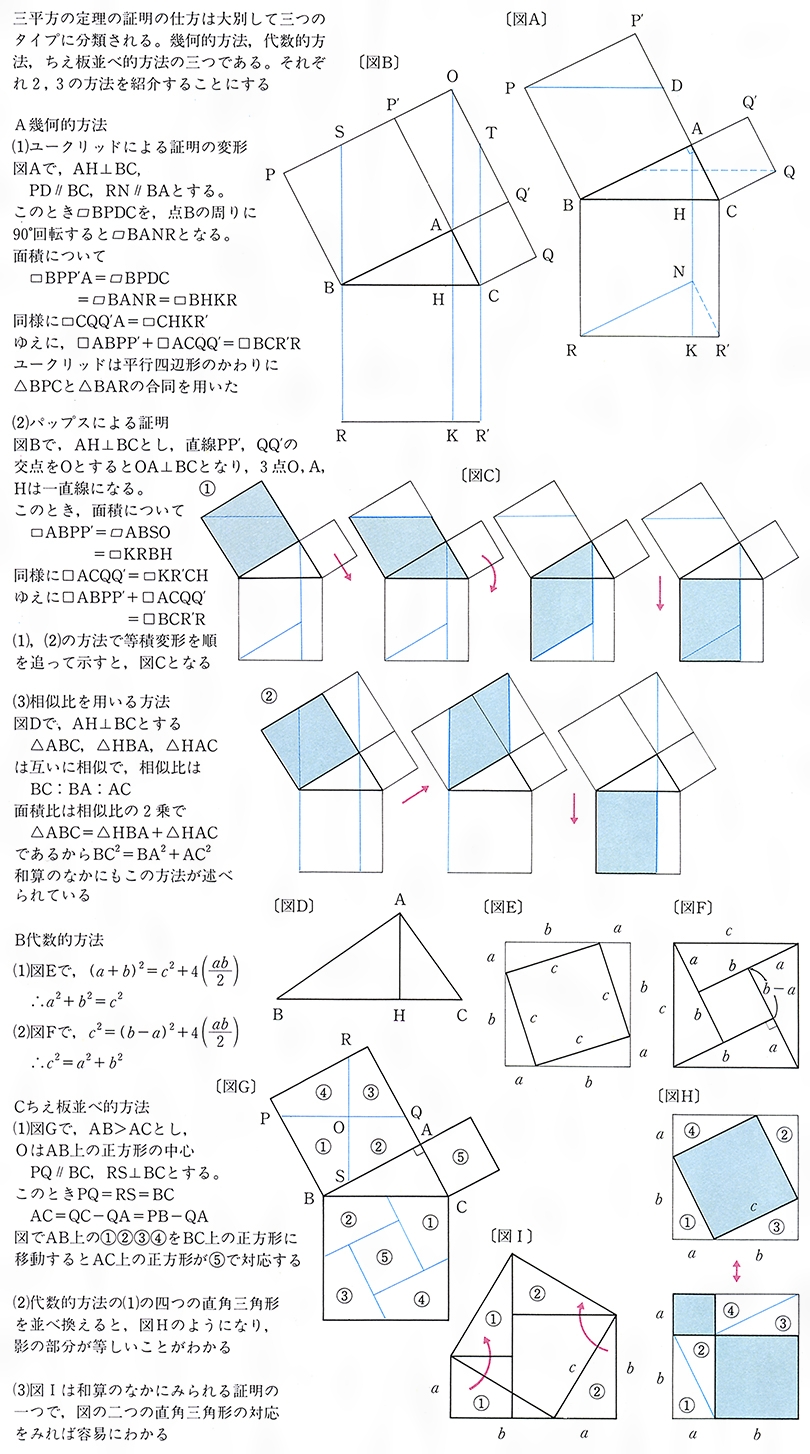



三平方の定理とは コトバンク




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



三平方の定理




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理の証明と使い方




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



ピタゴラスの定理 三平方の定理 の証明 Geogebra



1




ピタゴラスの定理 三平方の定理 ベクター イメージマート




三平方の定理 無料で使える中学学習プリント




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




三平方の定理の練習問題10問 解き方の解説 数学fun




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




ピタゴラスの定理 三平方の定理 のイラスト イラスト素材 フォトライブラリー Photolibrary




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



1




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理の4通りの美しい証明 高校数学の美しい物語




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース



3



ピタゴラスの定理とその証明



三平方の定理で底辺の二乗と高さの二乗をたせば どう考えたって斜辺の二乗になるに決まってるじゃん ほらなと中坊に簡単にうなずかせて解らせる方法を教えて下さいますか Quora




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
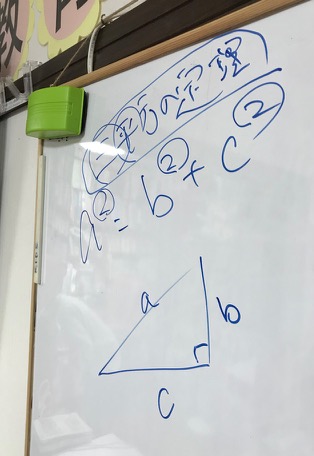



ピタゴラスの定理 三平方の定理 カタカナ語と日本語について考える たのしい教育研究所 沖縄 公式サイト
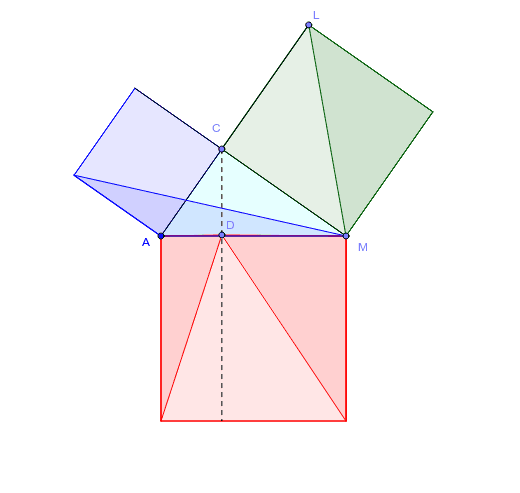



ピタゴラスの定理 ユークリッドの証明 Geogebra




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学
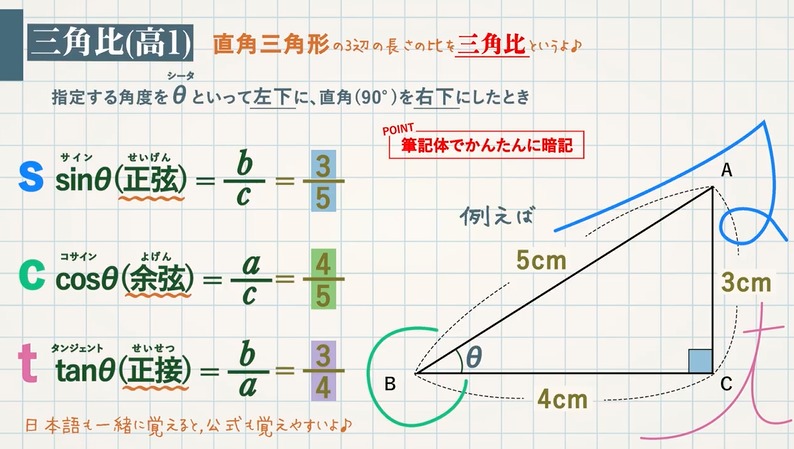



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube
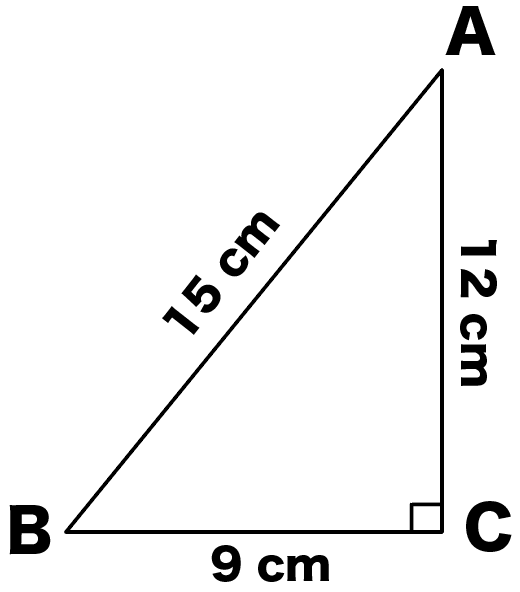



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4
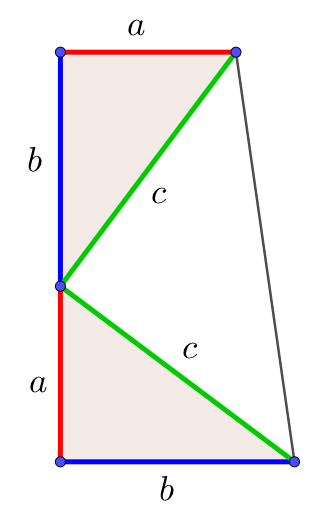



三平方の定理の証明3 大統領の台形 キソカラ
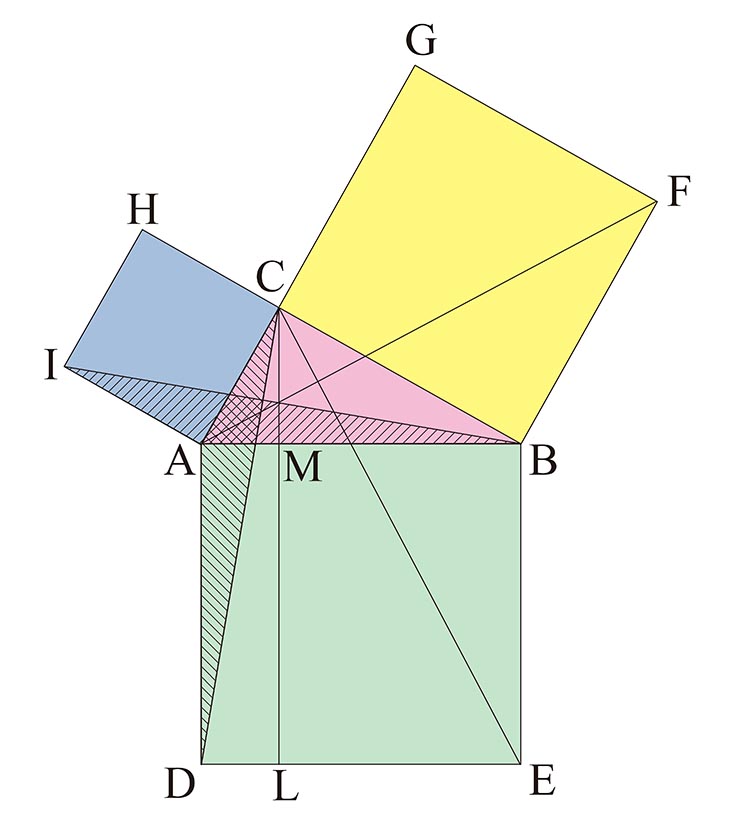



コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



三平方の定理




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理 ピタゴラスの定理




三平方の定理の証明と使い方




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




数学 中3 61 三平方の定理 基本編 Youtube



三平方の定理




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題


