Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes31 3 Separable differential Equations A differential equation of the form dy dx = f(x,y) iscalledseparableifthefunctionf(x,yBecause x is the independent variable, d dxx2 = 2x But y is the dependent variable and y is an implicit function of x Recall Example2, where we computed d dxf(x)2 Computing d dxy2 is the same and requires the chain rule, by which we find that d dxy2 = 2y1dy dx We now have that 2x 2ydy dx = 0
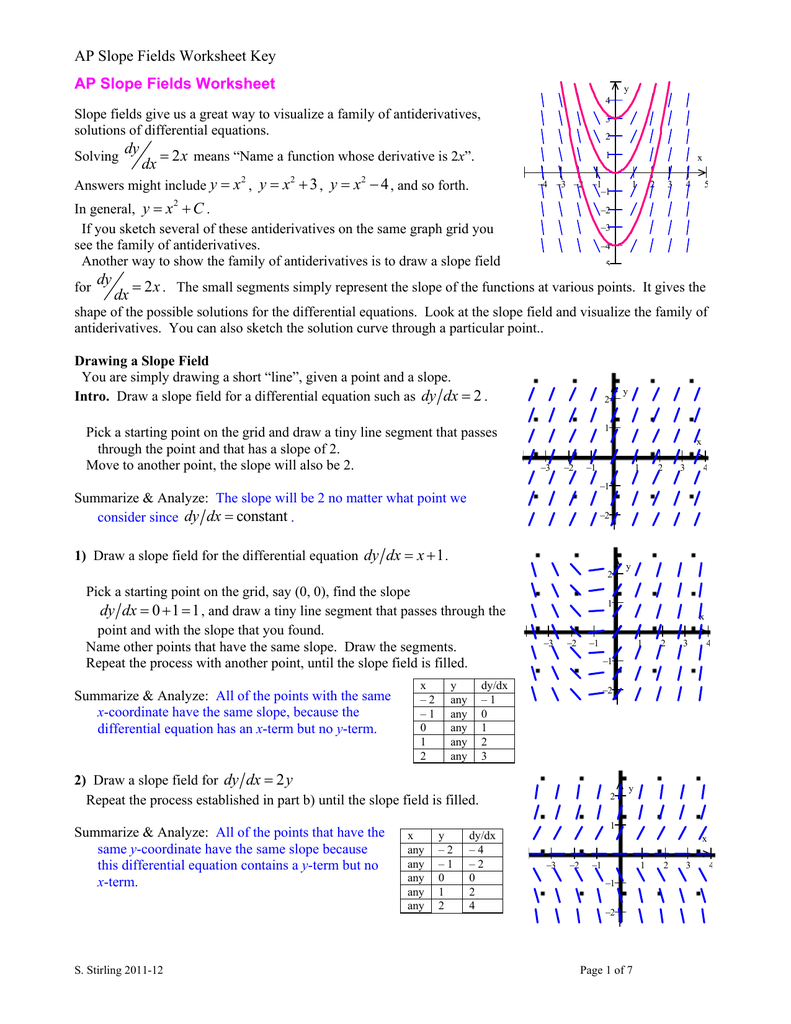
Ap Slope Fields Worksheet Key
Dy/dx=x^2+y^2 graph
Dy/dx=x^2+y^2 graph-Solve dy/dx=2xy/(x^2y^2) check_circle Expert Answer Want to see the stepbystep answer?X^2y^2=1 ;centered on the origin (0,0) with a radius of 1 ;problem find dy/dx, we'll use the chain rule du/dx= (du/dy) ( dy/dx) and let u=y^2 ;



Implicit Differentiation
Using the fact that du/dy = 2y, du/dx=2y dy/dx 2x 2y dy/dx = 0 ;Cry Insights Blog Browse All Articles Physics Articles Physics Tutorials Physics Guides Physics FAQ Math Articles Math Tutorials Math Guides Math FAQ Education Articles Education Guides Bio/Chem Articles Technology GuidesWelcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries
This equation is a Bernoulli equation as it can be rewritten to the form dy dx f (x)y = g(x)yn From x dy dx y = x2y2, one can divide both sides by x so that it fits the Bernoulli form dy dx y x = xy2 Divide both sides by y2 y−2 dy dx 1 xy = x Then, define a function v = y1−2 = y−1Find the solution of the differential equation that satisfies the given initial conditiondy/dx = y^2 1, y(1) = 0= Write an equation for the line tangent to the graph of y fx = ( ) at x =2 Use your equation to approximate f (21 ) (c) Find the particular solution y fx = ( ) to the given differential equation with the initial condition f (2 3) = (a) {1 zero slopes 2 1 nonzero slopes
Solve for dy/dx dy/dx = (1 y 2) / (4y 3 2xy) Example 3 Find all points on the graph of the equation x 2 y 2 = 4 where the tangent lines are parallel to the line x y = 2 Solution to Example 3 Rewrite the given line x y = 2 in slope intercept form y = x 2 and identify the slope as m = 1 The solution of the differential equation dy/dx = (x^2 xy y^2)/x^2, is asked May in Differential Equations by Rachi (296k points) differential equations;1 y 2 dy dx dx = Z 1 1y(x) y′(x)dx = Z 1 1 y2 dy , which, after cutting out the middle, reduces to Z 1 1 y 2 dy dx dx = Z 1 1 y dy , the very equation we would have obtained if we had yielded to temptation and naively "cancelled out the dx's" Consequently, the equation obtained by integrating both sides of equation (44) with



Http Howellkb Uah Edu Public Html Detext Part2 Separable Pdf



Increasing And Decreasing Ppt Download
The slopes at several points on the graph are shown below the graph y x dy dx 2x 3y2 2y 5 dy dx 3y2 2y 5 dy dx 3y2 2y 5 2x dy dx 3y2 dy dx 2y dy dx 5 dy dx 2x dy dx 3 y2 dy dx 2y dy dx 5 dy dx 2x 0 d dx y3 d dx y2 d dx 5y d dx x2 d dx 4 d dx y3 y2 5y x2 d dx 4 x dy dx x2 y2 4 dy dx 142 Chapter 2 Differentiation x 1 1 −1 −1 (0, 0Y = xn dy/dx = n xn1 y = a xn dy/dx = a n xn1 f (x) = a xn f' (x) = a n xn1 y = ex dy/dx = ex y = ea xMath Consider the differential equation dy/dx = 1 (y^2/ x)



6 Find Dy Dx If X 2 Y 2 2xy A X 1 Y B Chegg Com



1
So,the 'y' in the question,arcsin (2x/1x^2) is a little difficult to handle,so a smart substitution has been done in the form of x=tanθ which simplifies the 'y' to be equal to 2 arctan (x) Now,y=2tan^1 (x) Differentiating both sides,we get dy/dx=2*1/1x^2 as derivative of tan^1 (x) is 1/1x^2Solve first grade ecuation with bernoulli dy/dx = (y^22xy)/x^2general ecuation and particular when y(1)=1 1 Educator answer eNotescom will help you with any book or any questionA first order Differential Equation is Homogeneous when it can be in this form dy dx = F ( y x ) We can solve it using Separation of Variables but first we create a new variable v = y x v = y x which is also y = vx And dy dx = d (vx) dx = v dx dx x dv dx (by the Product Rule) Which can be simplified to dy dx = v x dv dx




The Graph Of A Function Y F X Is Shown At Which Point S Are The Following True A Dy Dx And D 2y Dx 2 Are Both Positive B Dy Dx And D 2y Dx 2 Are Both Negative C



How Do L Solve The Initial Value Problem X 2 Y 2 Dy Dx Xy Y 1 2 Quora
I found this initial value problem and was supposed to comment on the accuracy of Runge Kutta method Please enlighten me on the analytic solution Find y(2) given the differential equation \\frac{dy}{dx}=y^{2}x^{2} and the initial value y(1)=0 Thank you Find dy/dx for the equation x^32x^2y3xy^2=38 asked in CALCULUS by andrew Scholar derivatives implicitdifferntiation 2 If that's what it really says, your textbook is wrong The general solution of dy dx = x2 y2 is y(x) = − x(cJ − 3 / 4(x2 / 2) Y − 3 / 4(x2 / 2)) cJ1 / 4(x2 / 2) Y1 / 4(x2 / 2) where Jν and Yν are Bessel functions of the first and second kinds, and c is an arbitrary constant Share




Solve The Initial Value Problems X 2 Dy Dx 4x 2 Chegg Com




1 X 2 Dy Dx Xy 1 Youtube
See Answer Check out a sample Q&A here Want to see this answer and more?If x = 5, y = 2(5) 6 = 4 We then note that the graph of (5, 4) also lies on the line To find solutions to an equation, as we have noted it is often easiest to first solve explicitly for y in terms of x Example 2 Graph x 2y = 4 Solution We first solve for y in terms of x to getThis is a separable differential equation \frac {dy} {dx}=\frac {y^2} {x^29} \frac {1} {y^2} dy=\frac {dx} {x^29} Integrating both sides, \int \frac {1} {y^2} dy=\int \frac {dx} {x^29} The This is a separable differential equation dxdy = x29y2
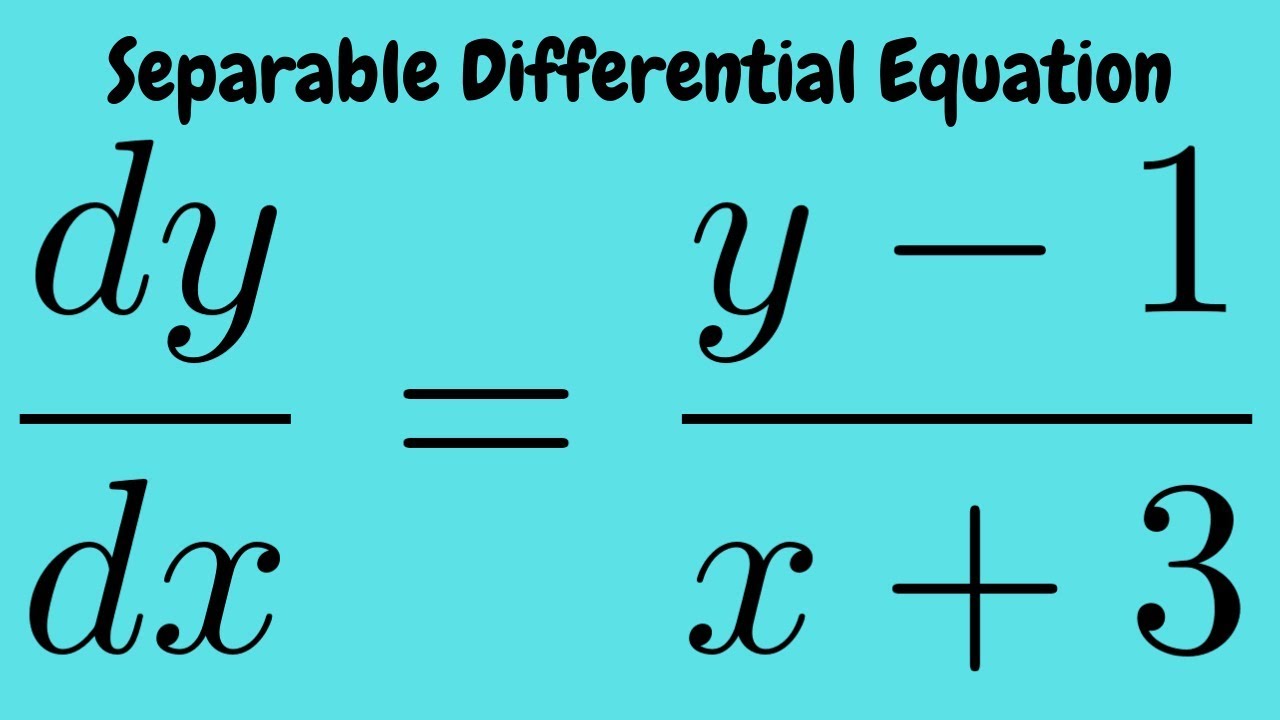



Initial Value Problem Dy Dx Y 1 X 3 With Y 1 0 Separable Differential Equation Youtube




Slope Fields Geogebra
Experts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!*By differentiating both sides with respect to x dy/dx = 2x / (2 (y) = x/yCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Search Q Differential Equations Tbm Isch




X 2 Y 2 3xy D Dx Dx 10y Dy Dx 2xy2 3y Pdf Free Download
The solutions to the differential equation dy/dx = x^2 y^2 1 are increasing at every point True False Suppose that y = f(x) is a solution of the differential equation dy/dx = 2x y, Determine if the following are true or false If f(a) = b, the slope of the graph of f at (a, b) is 2a b Let y = f(x) be the solution to the differential equation dy/dx=yx The point (5,1) is on the graph of the solution to this differential equation What is the approximation of f(6) if Euler's Method is used given ∆x = 05?Calculus Find dy/dx y^2=1/ (1x^2) y2 = 1 1 − x2 y 2 = 1 1 x 2 Differentiate both sides of the equation d dx (y2) = d dx ( 1 1−x2) d d x ( y 2) = d d x ( 1 1 x 2) Differentiate the left side of the equation Tap for more steps




Differential Equations Separation Of Variables Ppt Download




Solutions To Implicit Differentiation Problems
Solve the Differential Equation dy/dx=xy^2 In this tutorial we shall evaluate the simple differential equation of the form d y d x = x y 2 by using the method of separating the variables The differential equation of the form is given as d y d x = x y 2 Separating the variables, the given differential equation can be written asA) Solve the differential equation dy dx = x2 y2 b) Find the solution of this equation that satisfies the initial condition y(0) = 2 (UofO) MAT1322 C Differential Equations Winter 38 / 67 Separable Equations Solution a) We write the equation in terms of differentials and integrate both sides y2 dy = x2 dxZ y2 dy = Z x2 dx 1 3y3 = 1Calculus Integral with adjustable bounds example Calculus Fundamental Theorem of Calculus



How To You Find The General Solution Of Dy Dx X Y Socratic



Rules Of Calculus Functions Of One Variable
The differential equation is given as, {eq}{x^2}dy \left( {{y^2} xy} \right)dx = 0 {/eq} To find the solution of differential equation, Rewrite the given equation as, if y = log tan (∏/4 x/2) show that dy/dx = sec x donot go shortcut if y = log (x (1 x 2) 1/2 ) prove that dy/dx = 1/log (x (1 x 2) 1/2) 1/ (1 x 2) 1/2 Find dy/dx y = x x e (2x 5) mention each and every step Find dy/dx (x) 1/2 (y) 1/2 = (a) 1/2 Mention each and every step If y = tan 1 a/x log (xa/xa) 1/2, prove Solve the linear equation dy/dxy/x=x^2 Latest Problem Solving in Differential Equations More Questions in Differential Equations Online



Answered Which Of The Following Are Solutions To Bartleby




Solve Dy Dx X 2 3y 2 2xy Youtube
dy/dx=x^2(y1) dy/dx=x^2(y1) Math Calculus Physics Trigonometry Pre Calculus Limits Graph Graphing Integrals Derivative Area Volume Ap Calc Ab Calculus Calc Integral Math Word Problem Antiderivative Derivatives Introduction To Limits RELATED QUESTIONS find the derivative of Answers 1DEFINITION A differential equation is separable if it is of the form y'=f (x,y) in which f (x,y) splits into a product of two factors, one depending on x alone and the other depending of y alone Thus each separable equation can be expressed in the form y'=Q (x)R (y), where Q and R are given functions When R (y)0 we can divide by R (y) andView interactive graph > Examples separable\y'=e^{y}(2x4) separable\\frac{dr}{d\theta}=\frac{r^2}{\theta} x\frac{dy}{dx}=y^{2} en Related Symbolab blog posts Advanced Math Solutions – Ordinary Differential Equations Calculator, Linear ODE Ordinary differential equations can be a little tricky In a previous post, we talked about a




Ap Slope Fields Worksheet Key
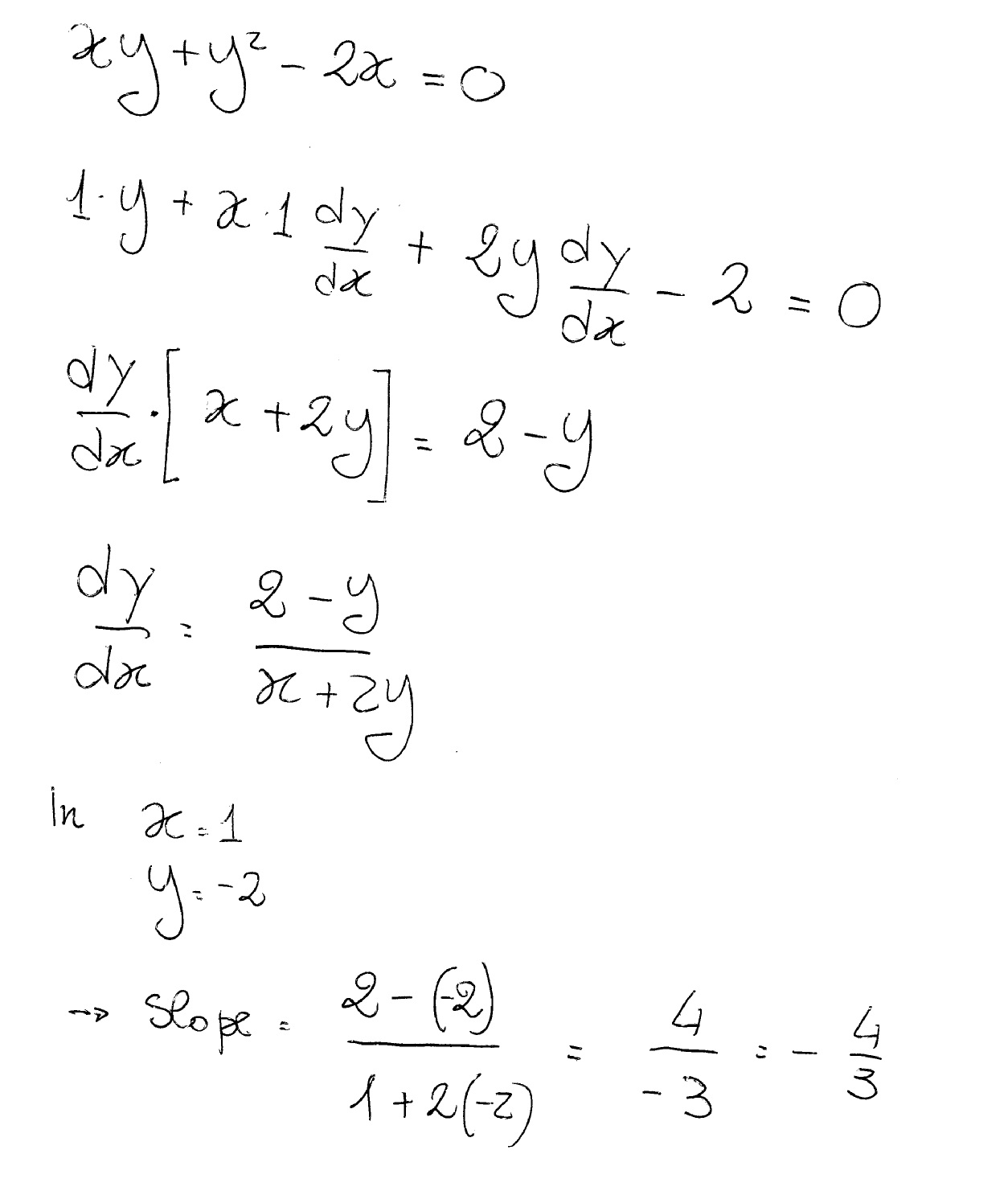



How Do You Differentiate Implicitly Xy Y 2x 0 To Find Dy Dx And Find The Slope Of The Curve At The Given Point 1 2 Socratic
The equation of a circle can be written as x2y2 = a2 x 2 y 2 = a 2 To compute the derivative, we've used implicit differentiation and used the common derivative d dx(xn) = nxn−1 d d x ( x nCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySince 2 2 is constant with respect to x x, the derivative of 2 2 with respect to x x is 0 0 2 x 0 2 x 0 Add 2 x 2 x and 0 0 2 x 2 x 2x 2 x Reform the equation by setting the left side equal to the right side y' = 2x y ′ = 2 x Replace y' y ′ with dy dx d y d x dy dx = 2x d y d x = 2 x
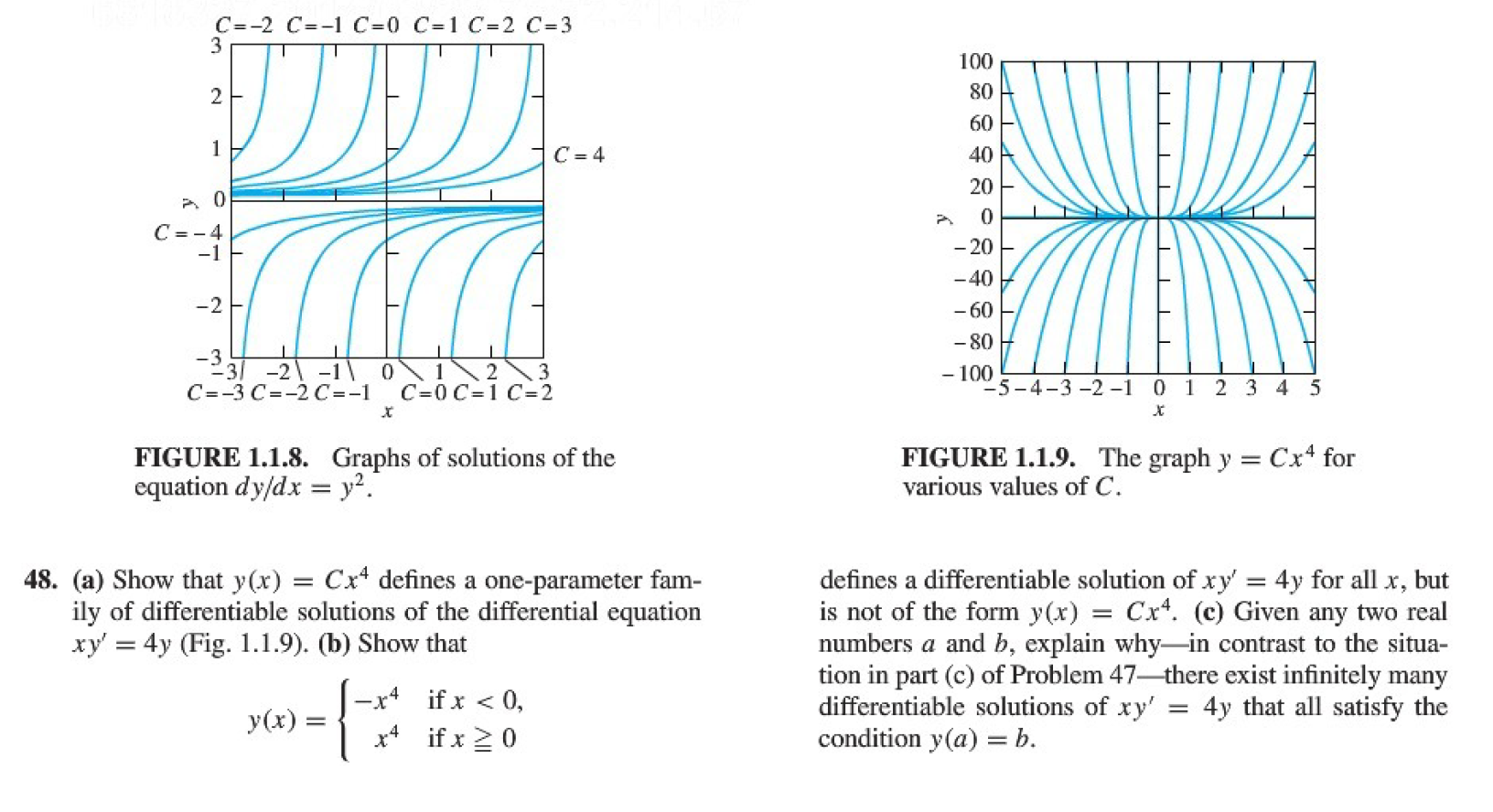



Graphs Of Solutions Of The Equation Dy Dx Y 2 Chegg Com




If Y 3x 2 2x Then Find Dy Dx
Consider Equation 272 and view y as an unknown differentiable function of x Differentiating both sides Equation 272 with respect to x, we have d dxx2 y2 = d dx16 On the right side of Equation 273, the derivative of the constant 16 is 0, and on the left we can apply the sum rule, so it follows thatSimple and best practice solution for (x^2xyy^2)dx(xy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it How to solve the differential equation dy/dx=xyy^2 In my case this leads to an integral which is unsolvable!



How To Solve This Differential Equation Dy Dx X 2y Quora




Implicit Differentiation
In calculus, Leibniz's notation, named in honor of the 17thcentury German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent infinitely small (or infinitesimal) increments of x and y, respectively, just as Δx and Δy represent finite increments of x and y, respectively Consider y as a function of a variable x, or y = f(x) If this is the case, thenD y d x = x − y x 2 y y ( 0) = 1 Note that solving this exact equation will lead to an implicit formula for y which will have two solutions for x = 2 However, the initial value problem has a unique solution and so just one of the two solutions produced from the implicit formula will be the actual value of y ( Show that the given differential equation is homogeneous x^2(dy/dx) = x^2 2y^2 xy asked in Differential Equations by KumkumBharti (
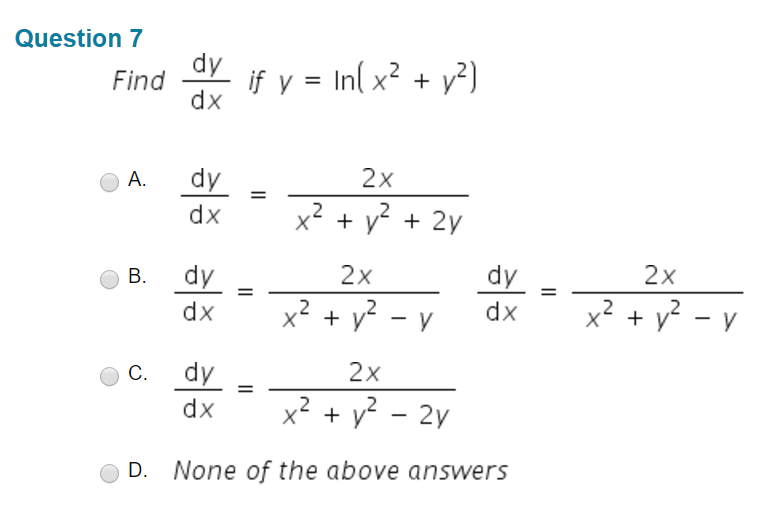



Find Dy Dx If Y In X 2 Y 2 Dy Dx 2x X 2 Chegg Com



Www Lcps Org Cms Lib Va Centricity Domain 2 5 notes filled out Pdf
We are asked to solve the differential equation (x − y) dy dx = x 2y We rearrange a little dy dx = x 2y x −y dy dx = 1 2(y x) 1 − (y x) (I) While I may not need to mention this, this differential equation is what is called a homogeneous differential equation I'll Let y = f(x) be the solution to the differential equation dy/dx=yx The point (5,1) is on the graph of the solution to this differential equation What is the approximation of f(6) if Euler's Method is used given ∆x = 05?Solve the differential equation `xy dy/dx = x^2 2y^2`




Implicit Differentiation




A Solution Of Dy Dx X Y Download Scientific Diagram
You haven't provided much information but here are two possible ways of solving it Solution one This is assuming you know at least one point on the integrated graph d y d x = x 2 − y 2 y = ∫ x 2 − y 2 d x y = ( x 3) 3 y 2 x c The following is where you should solve for c if you have your point, I am just going to carry it throughMultiply by y/y first Note from our relation 2y^2\log yx^2=0 that adding x^2 to both sides yields 2y^2\log y=x^2 Substitute for 2y^2\log y and you are done \begin{align*}\frac{dy}{dx}&=\frac{x}{2y\log yy}\\&=\frac{xy}{2y^2\log yy^2}\\&=\frac{xy}{x^2y^2}\end{align*}Dy/dx = x^2 y and y(2) = 2 (a) Use Picard's Theorem to show that the initial value problem has a unique solution (b) Verify that y(x) = 2 2x x2 is a solution to the initial value problem (c) Let h = 01 Use Euler's Method to estimate y(8) (Uses 100 steps)




What Is The Solution For Math Sqrt 1 X 2 Sqrt 1 Y 2 Dx Xy Dy 0 Math Quora




The Graph Of A Function Y F X Is Shown At Which Points Are The Following True Frac Dy Dx And Frac D 2y Dx 2 Are Both Negative Frac Dy Dx Is Negative But Frac D 2y Dx 2 Is Positive Study Com
Math Consider the differential equation dy/dx = 1 (y^2/ x)




Math 340 Lab
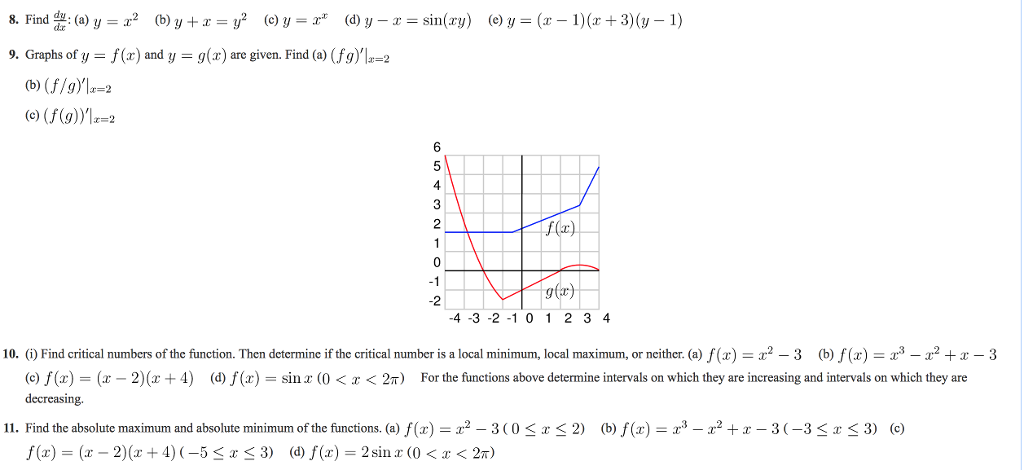



Find Dy Dx A Y X 2 B Y X Y 2 C Y X X Chegg Com
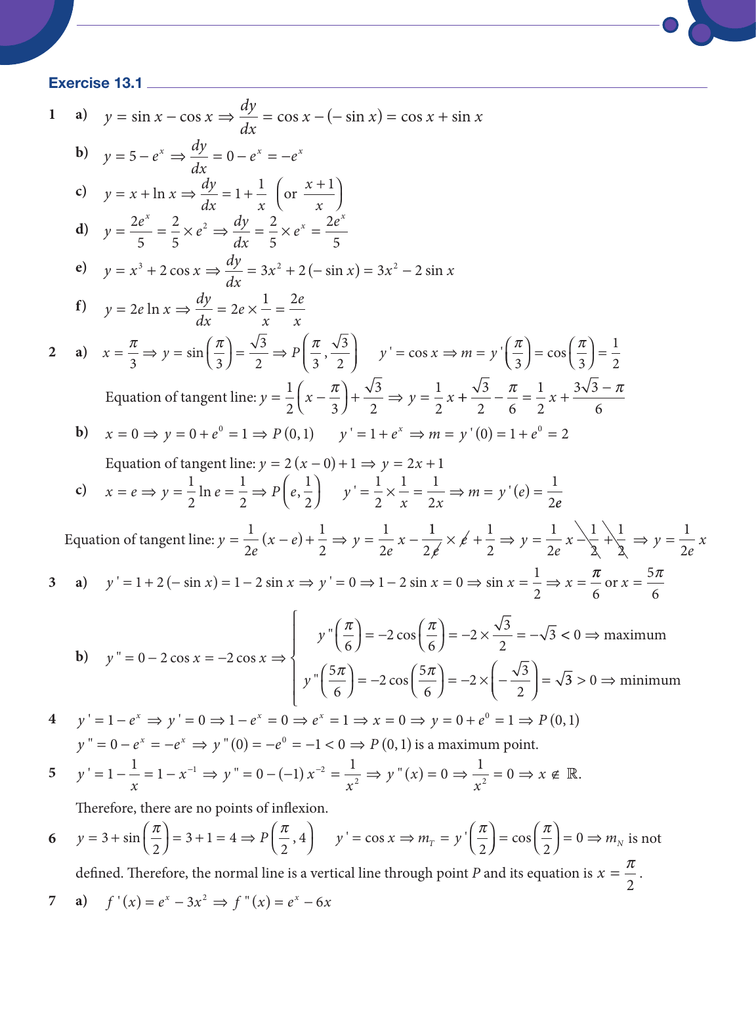



X X Dy Dx X X X X Sin Cos Cos Sin Cos Sin



Http Www Stewartcalculus Com Data Calculus 8e Demo Projects 08 14 Cengage Tec Publish Deployments Transcendentals 7e Support 022 Exercises Pdf




Implicit Differentiation



View Question The Expression Dy Dx X Y Gives The Slope At Any Point On The Graph Of The Function F X Where F 1 2



Implicit Differentiation
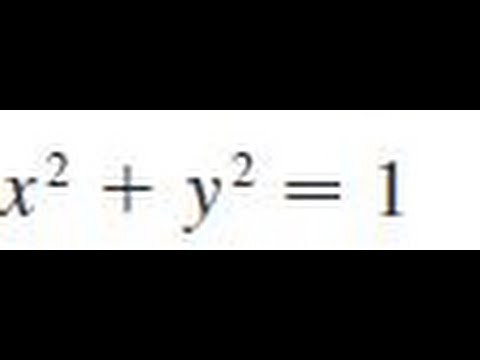



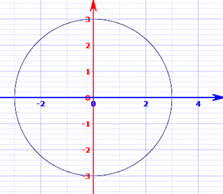
X 2 Y 2 1 Find Dy Dx By Implicit Differentiation Youtube



Solve The Differential Equation Math Y 2x Dfrac Dy Dx X X 1 Y 3 Math Quora




What Is The Solution Of Differential Equation D 2y Dx 2 2 Dy Dx Y 0 When X 0 Y 1 Dy Dx 2 Quora



4 2 Implicit Differentiation
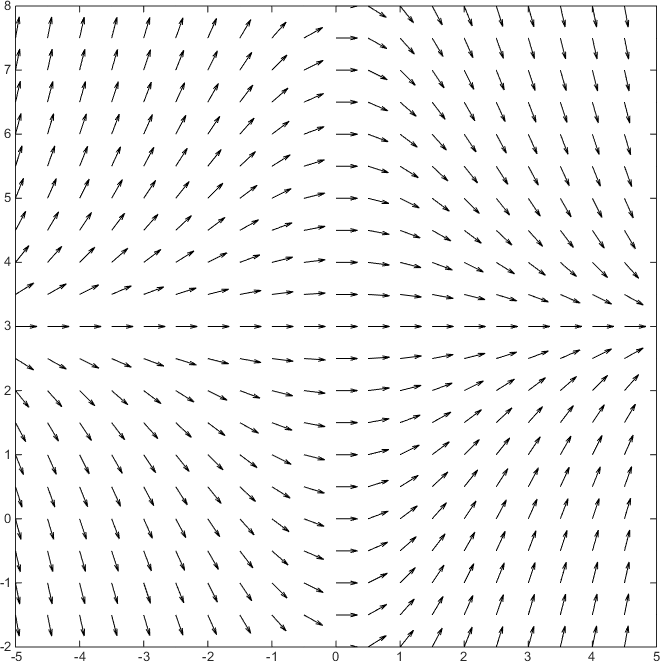



How Do You Draw The Slope Field Of The Differential Equation Dy Dx X 4 3 Y Socratic



Pchem Teaching Lab Maths




Solve The Differential Equation X 2 Dy Dx X Chegg Com




First Order Differential Equations Ppt Download




The Solution Of Dy Dx X 2 Y 2 1 2xy Satisfying Y 1 0 Is
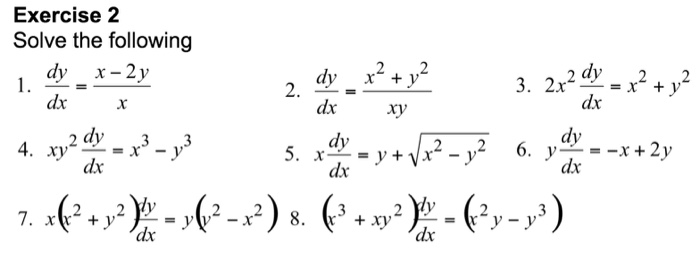



Solve The Following Dy Dx X 2y X Dy Dx X 2 Chegg Com



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




Implicit Differentiation
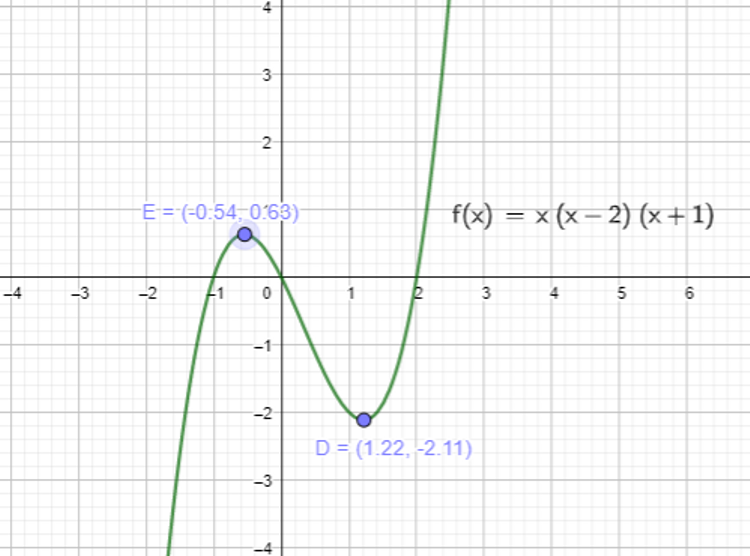



Basic Differentiation Tutorial For Igcse And A Level Maths Vivax Solutions




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib



Matlab Demo On 7 7 7 8 Differential Equations
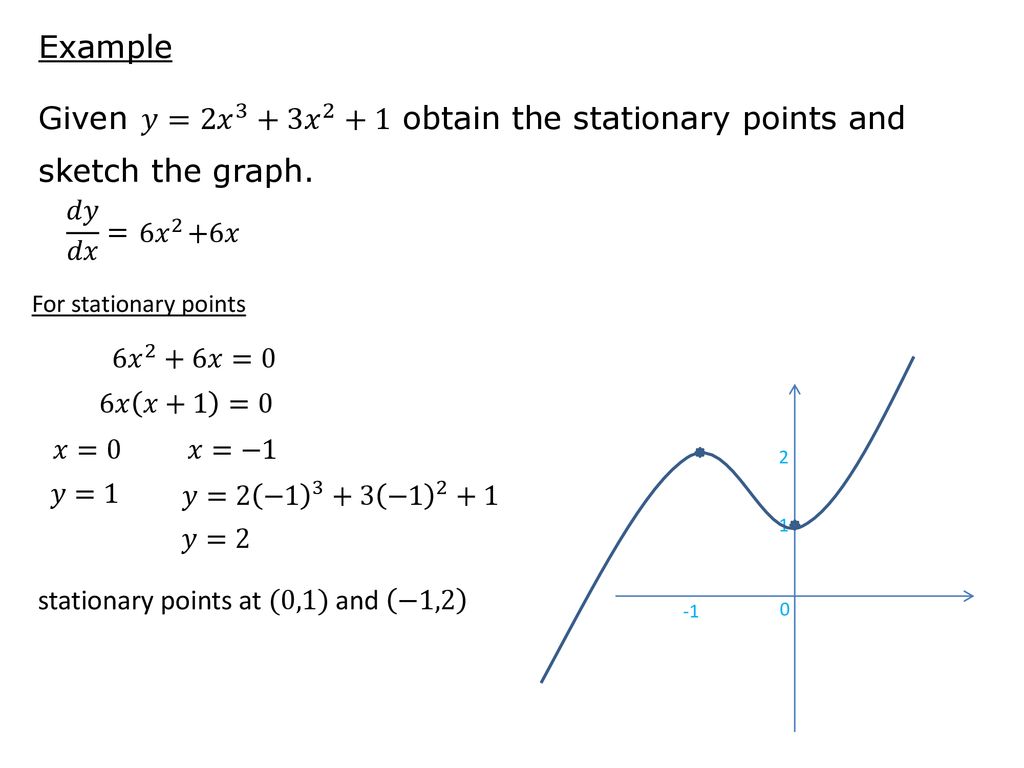



Stationary Points Saturday 24 November Ppt Download



Implicit Differentiation




Consider The Differential Equation Dy Dx 1 3x Y 2 2 A A Slope Field For The Given Differential Brainly Com



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf
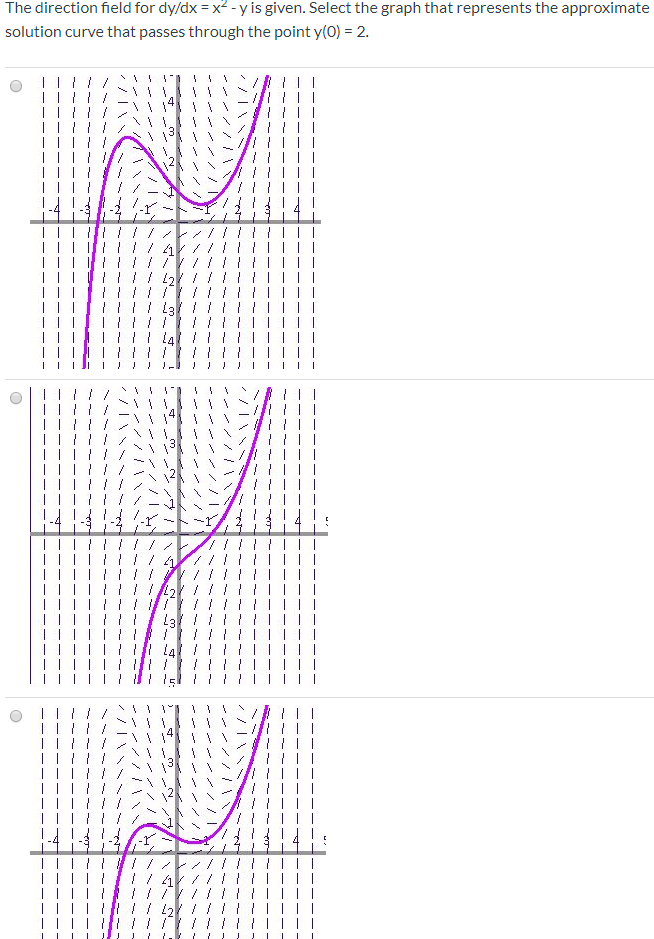



The Direction Field For Dy Dx X2 Y Is Given Select Chegg Com



The Direction Field For Dy Dx X2 Y Is Given Chegg Com



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau



Mathfunc



1



X Y 2 Y 2 Dx X 2 X 2 Y Dy 0 How Do You Solve The Differential Equation Quora




Math 432 Hw 2 5 Solutions Pdf Free Download




Integration Webfunpage Com



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf



How To Graph X 2 Dy Dx Y Xy Y 1 1 Quora




Implicit Differentiation Advanced Example Video Khan Academy




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download




Ex 9 4 16 For Xy Dy Dx X 2 Y 2 Find Solution
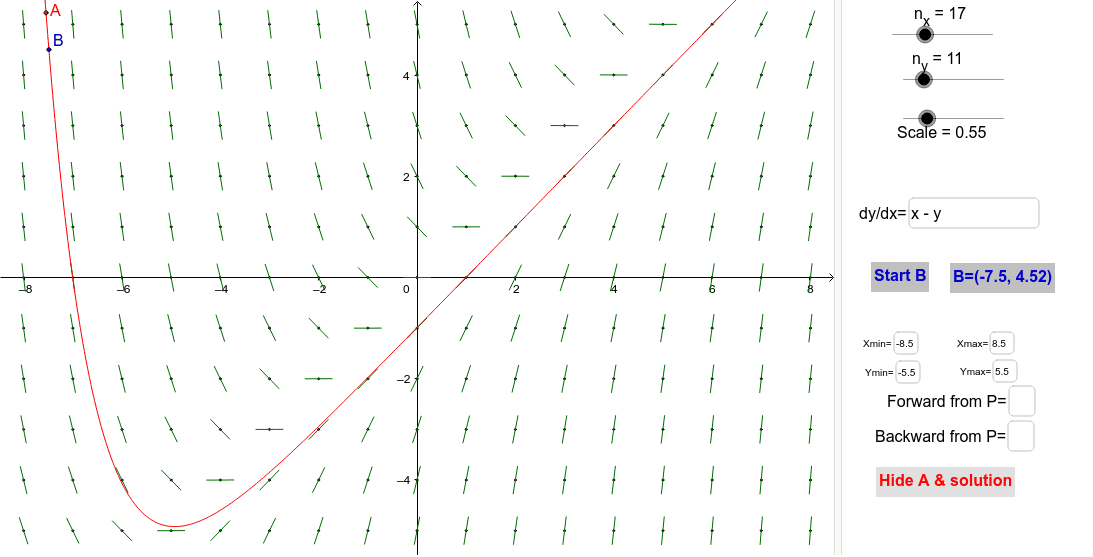



Slope Fields Geogebra



How To Solve Dy Dx X Y 1 X Y Quora




Ppt Drill Find Dy Dx Powerpoint Presentation Free Download Id




Find The Points On The Graph Of Y 2 X 3 3x 1 Where The Tangent Line Is Horizontal A First Show That 2yy 3x2 3 Where Y Dy Dx Study Com




A Solution Of Dy Dx X Y Download Scientific Diagram




Chapter 04
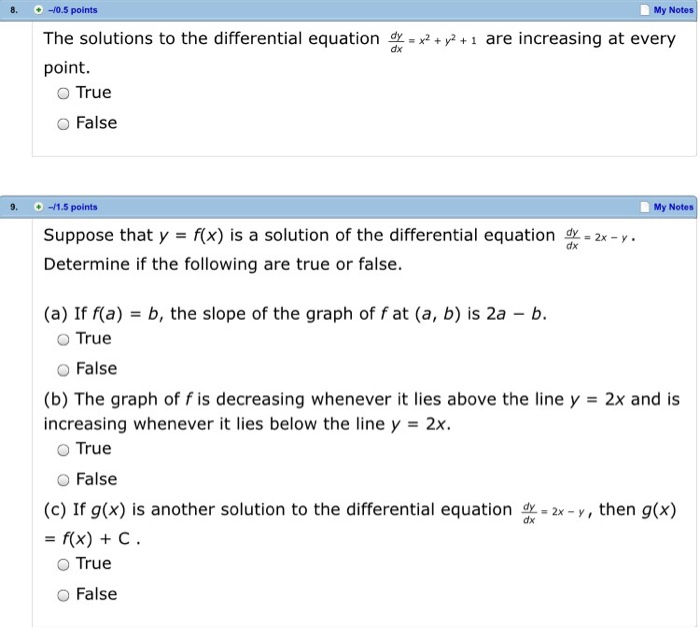



The Solutions To The Differential Equation Dy Dx Chegg Com



Slope Fields With Mathematica Exercise C 2



Http Pages Mtu Edu Ipinelis Teaching Ma3160 Review3 Key Pdf




Answered Sotuions Ii Part A Ane For Which Bartleby




Math 432 Hw 2 5 Solutions Pdf Free Download
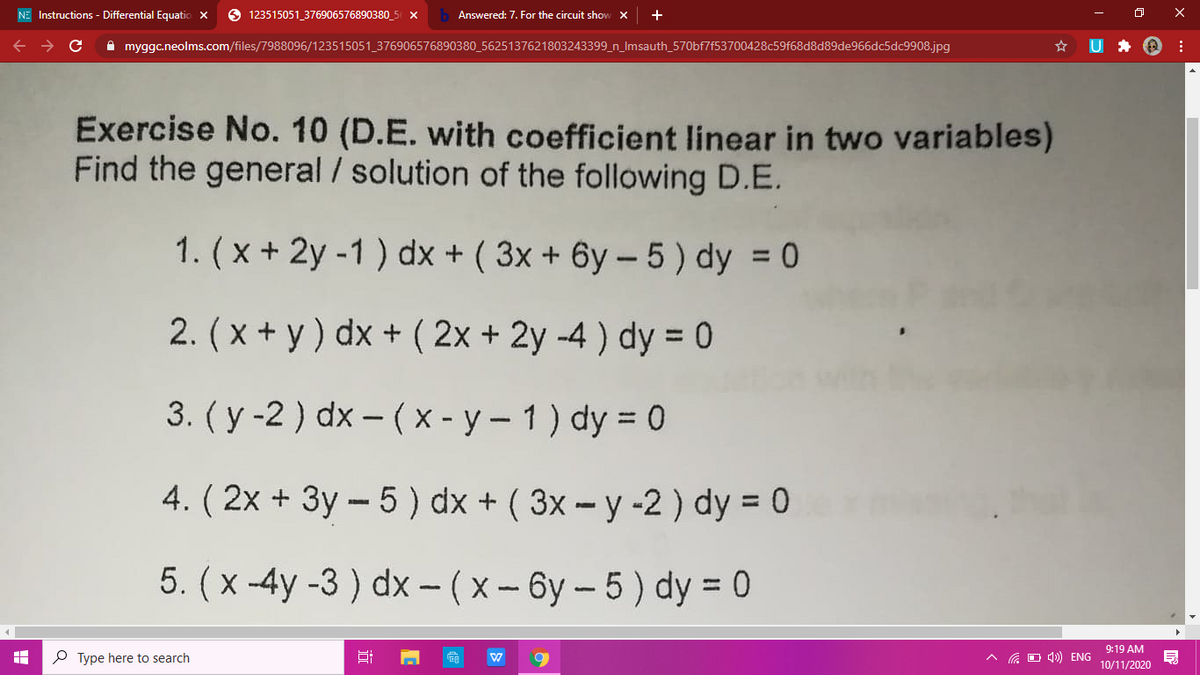



Answered 5 X 4y 3 Dx X 6y 5 Dy Bartleby



Matthew T Clay Sine Integral Function



How To Solve The Differential Equation Y X Dy Dx A Y 2 Dy Dx Quora



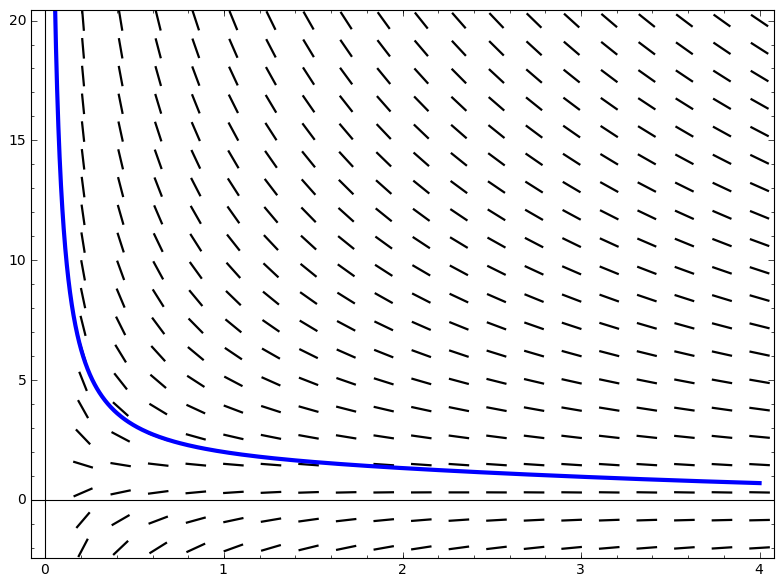
How Do You Draw The Slope Field Of The Differential Equation Dy Dx X 4 3 Y Socratic



How To Solve The Differential Dy Dx 4y 1 Given Y 0 When X 4 Quora




Why Do We Use Dy Dx In Ml By Satish Vavilapalli Issuu



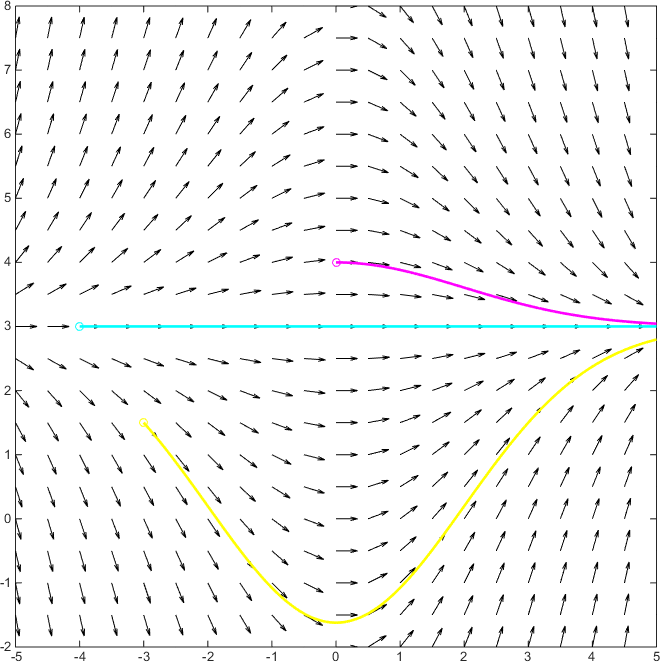
Answers To The Review Problems For The First Exam 251 05 10 In Spring 06



Basic Differentiation Tutorial For Igcse And A Level Maths Vivax Solutions




Documents Mx Eduv




How To Solve Math 1 X 2 Dy 1 Y 2 Dx Math Quora
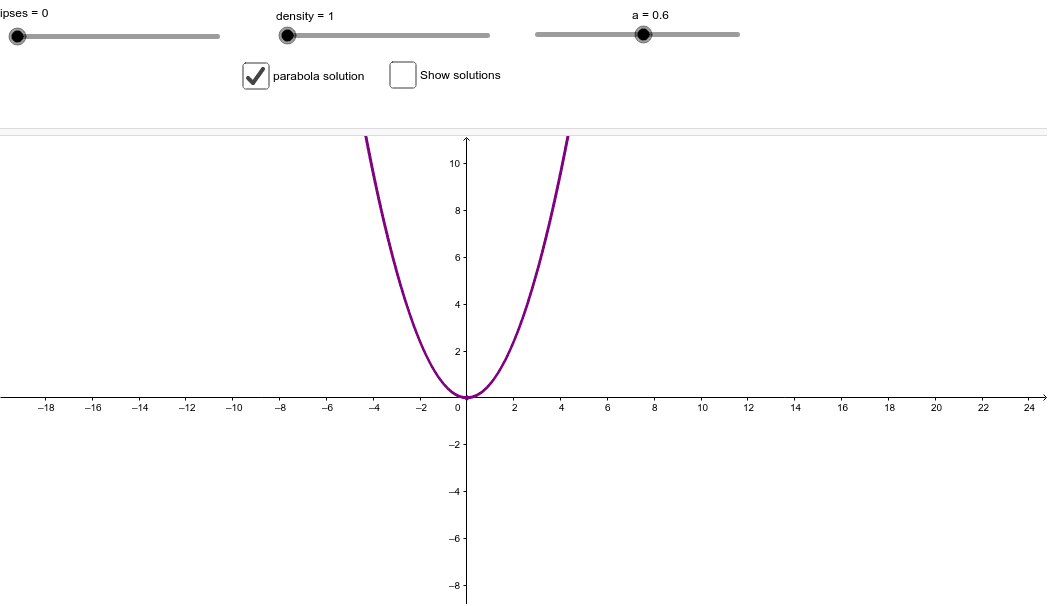



Dy Dx 2y X Geogebra




Solved Consider The Differential Equation Dy Dx 2x Y On The Axes Transtutors




Calculo 1 Given The Function Y 4 X 2 4 Arcsen X 2 Get Dy Dx Homeworklib
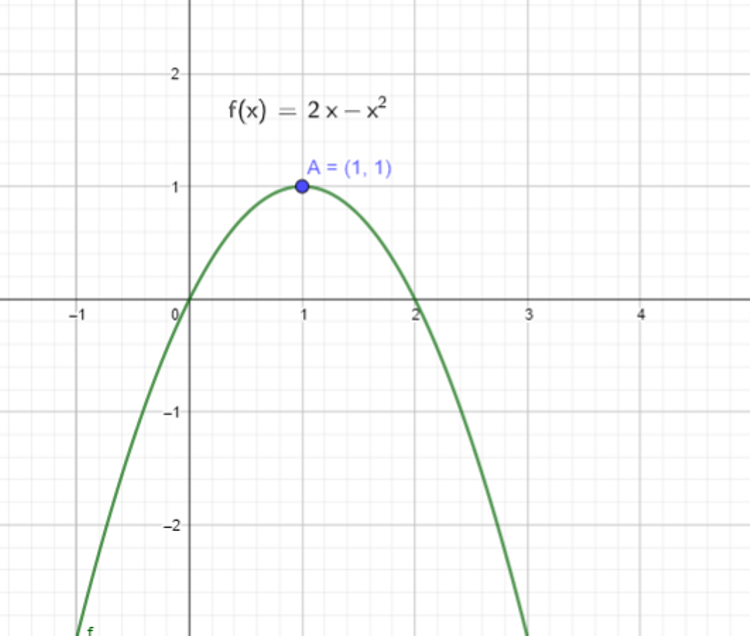



Basic Differentiation Tutorial For Igcse And A Level Maths Vivax Solutions




Slope Field Wikipedia




Differential Equations Separation Of Variables Ppt Download



Solution Find The Equation Of The Line Tangent To The Circle X2 Y2 25 At Point 3 4 Use The General Equation Of The Line For Your Final Answer




Differential Equations Separation Of Variables Ppt Download




Which Of The Following Is The Solution To The Chegg Com



4 2 Implicit Differentiation




Get Answer Consider The Differential Equation Dy Dx X 2y Let Y F X Be The Transtutors
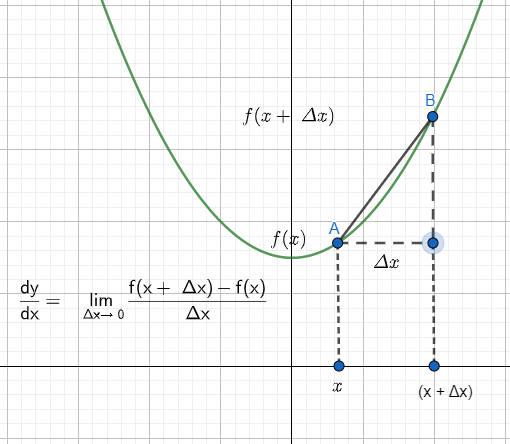



Basic Differentiation Tutorial For Igcse And A Level Maths Vivax Solutions



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q4 Pdf




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download


